- Download the video Dopplerball.m4v or better yet make your own.
- Go through the video frame by frame and determine the number of rotations per second.
- Using the radius of the circle calculate the tangential velocity
 of the ball.
of the ball. - Calculate the expected Doppler shifted frequencies from
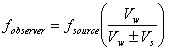
- Calculate an expected frequency as the ball comes toward you using the minus sign and as as the ball goes away using the plus sign. The speed of the wave is
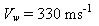 using data from the usual year-13 physics texts.
using data from the usual year-13 physics texts. - Download our sound file DopplerBall.wav taken from the video or extract the sound from your own video using video editing software (we use Ulead or QuickTime Pro. Neither of these are free but your camera may have come with suitable software.
- Use WavePad or similar software to find the spectrum over at least one full rotation when the ball is moving at pretty constant speed as indicated by the video file. The width of the spectrum gives the difference between the approaching ball frequency and the receding ball frequency. You will need to know the frequency of the source as well. This can be determined form a spectrum taken with the ball not moving relative to the camera.
Our numbers
Our camera takes 25 frames per second so the time per frame is 0.040 seconds. The ball made 6.0 rotations in 2.0 seconds with a radius of 0.9 metres (the radius has to be adjusted to take into account the motion of the hand). This gives us a radial velocity of 17 m/s. The source frequency is ![]() .
.
Using ![]() and
and ![]() we predict the difference in the approaching and receding to be
we predict the difference in the approaching and receding to be ![]() .
.
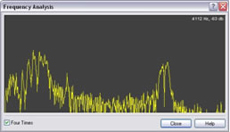
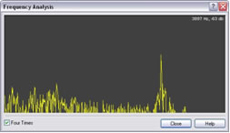
Using Wavepad to analyse the spectrum of a two second section of the sound recording from about six seconds to about eight seconds we find that the full width at half maximum of the spectrum is about 380 Hz. The two agree at least approximately. Note that estimating the range of frequencies in the spectrum involves some approximations. The spectrum is somewhat noisy and it is difficult to estimate the range. The full width at half maximum seems a reasonable approximation and gives rough agreement. See spectra below. The spectrum on the left shows the Doppler Shift as the ball moves toward and away from the observer.
The spectrum on the right does not show a Doppler Shift because the ball is moving in a circle but does not approach or recede from the observer.
Click here for larger annotated spectra.